树上差分

树上差分，顾名思义，就是在树上进行差分，以起到优化复杂度的目的。主要作用是对树上的路径进行修改和查询操作，在修改多、查询少的情况下复杂度比较优秀。

在一般情况下，树上差分一般分为点差分和边差分

点差分

例如，一个树初始状态下点权都是 $0$，要求对路径 $(x,y)$ 上的所有点做点权$+1$的操作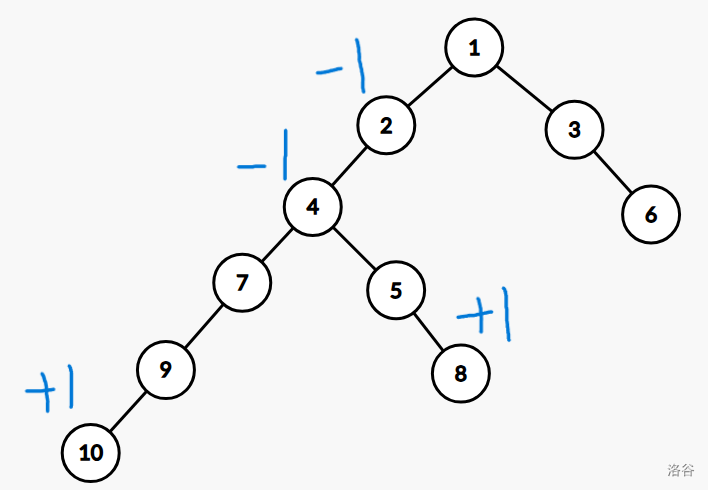如上图所示点差分操作等价于 ($d$ 表示点权)

$$ d_{10} + 1,d_{8} + 1,d_{4} - 1,d_{fa[4]} - 1 $$ 进行深搜递归，自底向上计算节点差分值的子树和，恰好使得 $(x,y)$ 路径上所有的点权为1，同时消除了对 $lca(x,y)$ 以上点的影响

在 $(10,4)$ 路径上 $d_{10}$ 的 $+1$ 和 $d_4$ 的$-1$ 相互抵消 $d_4$ 权值变为 $0$

在 $(8,4)$ 路径上 $d_8$ 的权值为 $1$，$d_4$ 的权值变为 $1$，从 $d_4$ 到 $d_{fa[lca(10,8)]} = d_2$ 的路径上 $d_4$ 的 $+1$ 和 $d_2$ 的 $-1$ 相互抵消，消除了对 $lca$ 以上的节点的影响

总结

处理 $(x,y)$ 路径上的点差分等价于 $$ d_x + 1,d_y + 1,d_{lca(x,y)}- 1,d_{fa(lca(x,y))}-1 $$

边差分

例如，一个树初始状态下各边边权都为 $0$，现对路径$(x,y)$ 上的边均做 $+1$ 操作

对边权的操作比较困难，通常把边权下移到节点，变成点权操作（因为一颗树只有 $n - 1$ 条边每一条边都可以固定绑在下一个点上，每个点下方的权值是其上方连接它的边的权值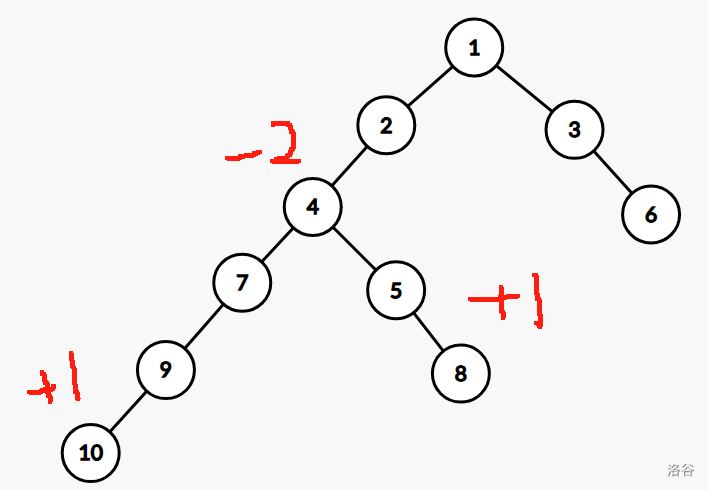）如上图所示，边差分操作等价于 $$ d_{10} + 1, d_8 + 1,d_4-2 $$ 进行深搜递归，自底向上计算节点差分值的子树和，恰好使得 $(x,y)$ 路径上所有的边权为1,同时消除了对 $lca(x,y)$ 以上路径的影响

过程同上

总结

处理路径 $(x,y)$ 上的边差分等价于 $$ d_x + 1,d_y + 1,d_{lca(x,y)}-2 $$

当树的初始都不为 $0$

以上所举的例子都是初始状态为0的情况，那如果初始状态不为 $0$ 呢

在初始状态不为 $0$ 的情况下，我们可以先计算出各点点权的差分值

叶子节点差分值=自己的点权

其他节点的差分值=自己点权值-子节点权值

之后再做差分操作，最后计算节点差分值的子树值

题目

P3128 [USACO15DEC] Max Flow P

使用LCA和树上差分求解此题

参考代码

#include<bits/stdc++.h>
using namespace std;
const int maxn = 5e5 + 10;

int n, k;
int cnt;
int head[maxn];
int quan[maxn]; 
int ans;

struct node{
    int to;
    int nxt;
}e[maxn];

void add(int u, int v){
    e[++cnt].to = v;
    e[cnt].nxt = head[u];
    head[u] = cnt;
}

int f[maxn][30], de[maxn];


void dfs(int u, int fa){
    de[u] = de[fa] + 1;
    f[u][0] = fa;
    for(int i = 1 ; i <= 27 ; i++){
        f[u][i] = f[f[u][i - 1]][i - 1];
    }
    for(int i = head[u] ; i ; i = e[i].nxt){
        int v = e[i].to;
        if(v != fa){
            dfs(v, u);
        }
    }
}

int lca(int u, int v){
    if(de[u] < de[v]){
        swap(u, v);
    }
    for(int i = 20 ; i >= 0 ; i--){
        if(de[f[u][i]] >= de[v]){
            u = f[u][i];
        } 
    }
    if(u == v){
        return v;
    }
    for(int i = 20 ; i >= 0 ; i--){
        if(f[u][i] != f[v][i]){
            u = f[u][i];
            v = f[v][i];
        }
    }
    return f[u][0];
}

void solve(int u, int fa){
    for(int i = head[u] ; i ; i = e[i].nxt){
        int v = e[i].to;
        if(v == fa){
            continue;
        }
        solve(v, u);
        quan[u] += quan[v];
    }
    ans = max(ans, quan[u]);
}

int main(){
    ios::sync_with_stdio(0),cin.tie(0);
    cin >> n >> k;
    for(int i = 1 ; i < n ; i++){
        int u, v;
        cin >> u >> v;
        add(u, v);
        add(v, u); 
    }
    dfs(1, 0);
    for(int i = 1 ; i <= k ; i++){
        int a, b;
        cin >> a >> b;
        int LCA = lca(a, b);
        ++quan[a];
        ++quan[b];
        --quan[LCA];
        --quan[f[LCA][0]];
    }
    solve(1, 0);
    cout << ans << endl;
    return 0;
}

其他题目

P10931 闇の連鎖

树上差分

点差分

总结

边差分

总结

当树的初始都不为 \(0\)

题目