跳转至

前缀和与差分

前缀和

定义

前缀和可以理解为一个数组前 \(n\) 项的和，常用于优化代码时间复杂度上。

C++ 标准库中实现了前缀和函数 std::partial_sum，定义于头文件 <numeric> 中。

一维前缀和

给定一个数组 \(a\)，维护一个前缀和数组 \(h\)，\(h_i\) 表示数组 \(a\) 中 \(a_1,a_2,...a_i\) 的和。 $$ \begin{align} h[n] = \sum_{i=1}^{n}a[i] \end{align} $$

1
h[i] = h[i - 1] + a[i];

求区间和

利用前缀和求一个区间的长度就非常的简单了，根据前缀和的定义可得 $$ \begin{align} S_{l,r} &= \sum_{i=l}^{r}a[i]\ &=h[r] - h[l-1] \end{align} $$

例题

P8218 【深进1.例1】求区间和

P3131

二维前缀和/多维前缀和

顾名思义，二维前缀和即维护二维数组前缀和

2前缀和.png

给定一个二维数组 \(a\)，维护一个前缀和数组 \(d\)。如果暴力计算的话，易得

\[ h[n][m]=\sum_{i=1}^n\sum_{j=1}^m a[i][j] \]

容斥思想求法

这样计算的话时间复杂度就爆炸了，那维护这个就没有起到优化的作用了，我们可以参考一维前缀和从 \(d[i - 1]\) 入手，二维前缀和我们可以从 \(d[i-1][j]\) 和 \(d[i][j-1]\) 入手，如上图所示，\(d[i][j]\) 可以从图中黄色+红色和橙色+红色部分转移过来，但是我们发现红色区域的 \(d[i-1][j-1]\) 计算了两遍，我们需要将多余计算的部分减去，再加上绿色部分（也就是 \(a[i][j]\) 本身）即可（该方法其实基于容斥原理思想实现）

\[ h[i][j]=h[i-1][j]+h[i][j-1]-h[i-1][j-1]+a[i][j] \]

逐维前缀和

对于一般的情形，给定 \(k\) 维数组 \(a\) 大小为 \(N\)，求其前缀和，易得

\[ h_{i_1,···,i_k}=\sum_{i'_1\leq i_1}···\sum_{i_k'\leq i_k} a_{i_1,···,i_k} \]

从上式可以看出，\(k\) 维前缀和就等于 \(k\) 次求和。所以，一个显然的算法是，每次只考虑一个维度，固定所有其它维度，然后求若干个一维前缀和，这样对所有 \(k\) 个维度分别求和之后，得到的就是 \(k\) 维前缀和。

利用逐维前缀和求二维前缀和的代码示例

1
2
3
4
5
6
for(int i = 1 ; i <= n ; i++)
    for(int j = 1 ; j <= n ; j++)
        h[i][j] += h[i - 1][j];
for(int i = 1 ; i <= n ; i++)
    for(int j = 1 ; j <= n ; j++)
        h[i][j] += h[i][j - 1];
例题

E - Or Plus Max

CF1208F

求区间和

前缀和求区间和.png

思想与上面的维护基本相同，要求上方绿色区域的和，由图易得，图中四块之和，减去黄色+红色和橙色+红色区域就剩下绿色了，但似乎红色区域被减了两次，将其加回来即可 $$ S_{x1,y1,x2,y2}=h[x2][y2]-h[x2-1][y2]-h[x2][y2-1]+h[x1][y1] $$

例题

P1387 最大正方形

P3397 地毯

HNOI2003 激光炸弹

差分

一维差分

前缀和，是维护和，那差分就是维护差咯，但与前缀和维护的有所不同，一维差分维护的是后一个元素与前一个元素的差。

给定一个数组 \(a\)，维护一个差分数组 \(d\)，易得 $$ d[i]=a[i]-a[i-1] $$

性质

\(1.\) 数组 \(a\) 的差分数组的前缀和数组就等于原数组 \(a\)，即 \(h[i]=a[i]=h[i-1]\ +\ d[i]\)

\(2.\) 数组 \(a\) 的前缀和的差分数组就等于原数组 \(a\)，即 \(d[i]=a[i]=h[i]\ -\ h[i-1]\)

\(3.\) 区间修改，这是差分数组最重要也是最常用的一条。当我们要将数组 \(a\) 上的某一区间 \([l,r]\) 加上 \(x\) 时，修改原数组较为麻烦，我们可以直接在差分数组上修改，且较为简单。将操作放在差分数组上，变为 \(d[l]\ +=\ x,d[r + 1]\ -=\ x\) ，这样，我们的操作就变为了单点操作，降低了时间复杂度。

例题

P2367

P4552

二维差分

根据二维前缀和公式和差分数组的定义，我们可以推出二维差分的公式。 $$ d[i][j]=a[i][j]-a[i-1][j]-a[i][j-1]+a[i-1][j-1] $$

性质

\(1.\) 二维差分的性质和一维相似，我们可以通过差分数组求出原数组。 $$ a[i][j]=d[i][j]+d[i-1][j]+d[i][j-1]-d[i-1][j-1] $$ \(2.\) 通过二维差分数组可以将区间修改改为几个单点操作。

二维差分.png

如上图所示，我们要在红色区域全部加上 \(x\)，在开始的 \((x1,y1)\) 处加 \(x\)，根据前缀和的性质，它影响的是全部四个颜色的区域，多影响了黄色+绿色和橙色+绿色两个区域，我们在这两个区域 \(-x\)，消除对其的影响，而且我们发现，右下角的绿色区域，被修改了两次，我们再在区间的左下角 \((x2,y2)\) 处 \(+x\)，即可。 $$ \begin{align} d[x1][y1]&+=x\ d[x1][y2+1]&-=x\ d[x2][y2]&+=x\ d[x2+1][y1]&-=x \end{align} $$

树上差分

树上差分，顾名思义，就是在树上进行差分，以起到优化复杂度的目的。主要作用是对树上的路径进行修改和查询操作，在修改多、查询少的情况下复杂度比较优秀。

在一般情况下，树上差分一般分为点差分和边差分

点差分

例如，一个树初始状态下点权都是 \(0\)，要求对路径 \((x,y)\) 上的所有点做点权\(+1\)的操作 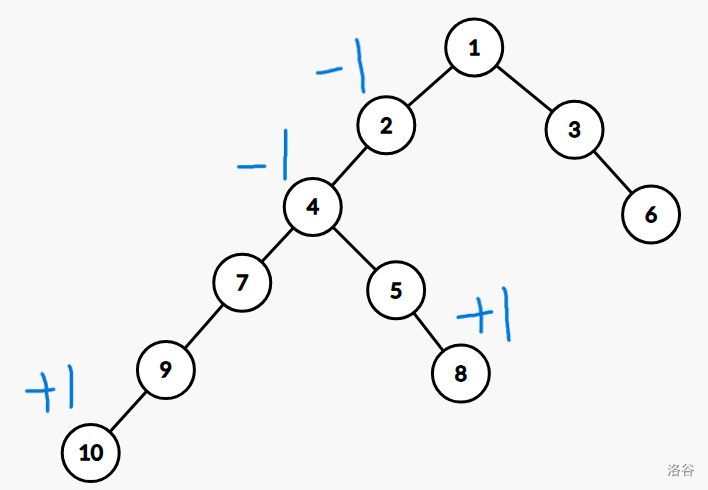如上图所示点差分操作等价于 (\(d\) 表示点权) $$ d_{10} + 1,d_{8} + 1,d_{4} - 1,d_{fa[4]} - 1 $$ 进行深搜递归，自底向上计算节点差分值的子树和，恰好使得 \((x,y)\) 路径上所有的点权为1，同时消除了对 \(lca(x,y)\) 以上点的影响

在 \((10,4)\) 路径上 \(d_{10}\) 的 \(+1\) 和 \(d_4\) 的\(-1\) 相互抵消 \(d_4\) 权值变为 \(0\)

在 \((8,4)\) 路径上 \(d_8\) 的权值为 \(1\)，\(d_4\) 的权值变为 \(1\)，从 \(d_4\) 到 \(d_{fa[lca(10,8)]} = d_2\) 的路径上 \(d_4\) 的 \(+1\) 和 \(d_2\) 的 \(-1\) 相互抵消，消除了对 \(lca\) 以上的节点的影响

总结

处理 \((x,y)\) 路径上的点差分 等价于 $$ d_x + 1,d_y + 1,d_{lca(x,y)}- 1,d_{fa(lca(x,y))}-1 $$

边差分

例如，一个树初始状态下各边边权都为 \(0\)，现对路径\((x,y)\) 上的边均做 \(+1\) 操作

对边权的操作比较困难，通常把边权下移到节点，变成点权操作（因为一颗树只有 \(n - 1\) 条边每一条边都可以固定绑在下一个点上，每个点下方的权值是其上方连接它的边的权值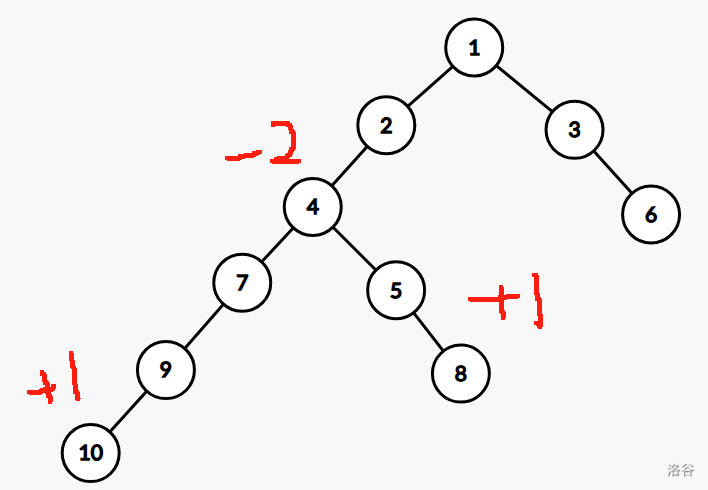） 如上图所示，边差分操作等价于 $$ d_{10} + 1, d_8 + 1,d_4-2 $$ 进行深搜递归，自底向上计算节点差分值的子树和，恰好使得 \((x,y)\) 路径上所有的边权为1,同时消除了对 \(lca(x,y)\) 以上路径的影响

过程同上

总结

处理路径 \((x,y)\) 上的边差分等价于 $$ d_x + 1,d_y + 1,d_{lca(x,y)}-2 $$

特殊情况 当树的初始都不为 \(0\)

以上所举的例子都是初始状态为0的情况，那如果初始状态不为 \(0\) 呢

在初始状态不为 \(0\) 的情况下，我们可以先计算出各点点权的差分值

叶子节点差分值=自己的点权

其他节点的差分值=自己点权值-子节点权值

之后再做差分操作，最后计算节点差分值的子树值

例题

P3128 [USACO15DEC] Max Flow P

使用 \(LCA\) 和树上差分求解此题

参考代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
#include<bits/stdc++.h>
using namespace std;
const int maxn = 5e5 + 10;

int n, k;
int cnt;
int head[maxn];
int quan[maxn]; 
int ans;

struct node{
    int to;
    int nxt;
}e[maxn];

void add(int u, int v){
    e[++cnt].to = v;
    e[cnt].nxt = head[u];
    head[u] = cnt;
}

int f[maxn][30], de[maxn];


void dfs(int u, int fa){
    de[u] = de[fa] + 1;
    f[u][0] = fa;
    for(int i = 1 ; i <= 27 ; i++){
        f[u][i] = f[f[u][i - 1]][i - 1];
    }
    for(int i = head[u] ; i ; i = e[i].nxt){
        int v = e[i].to;
        if(v != fa){
            dfs(v, u);
        }
    }
}

int lca(int u, int v){
    if(de[u] < de[v]){
        swap(u, v);
    }
    for(int i = 20 ; i >= 0 ; i--){
        if(de[f[u][i]] >= de[v]){
            u = f[u][i];
        } 
    }
    if(u == v){
        return v;
    }
    for(int i = 20 ; i >= 0 ; i--){
        if(f[u][i] != f[v][i]){
            u = f[u][i];
            v = f[v][i];
        }
    }
    return f[u][0];
}

void solve(int u, int fa){
    for(int i = head[u] ; i ; i = e[i].nxt){
        int v = e[i].to;
        if(v == fa){
            continue;
        }
        solve(v, u);
        quan[u] += quan[v];
    }
    ans = max(ans, quan[u]);
}

int main(){
    ios::sync_with_stdio(0),cin.tie(0);
    cin >> n >> k;
    for(int i = 1 ; i < n ; i++){
        int u, v;
        cin >> u >> v;
        add(u, v);
        add(v, u); 
    }
    dfs(1, 0);
    for(int i = 1 ; i <= k ; i++){
        int a, b;
        cin >> a >> b;
        int LCA = lca(a, b);
        ++quan[a];
        ++quan[b];
        --quan[LCA];
        --quan[f[LCA][0]];
    }
    solve(1, 0);
    cout << ans << endl;
    return 0;
}

P10931 闇の連鎖 题解

P3258

We will reach the shore eventually